CHAPTER 10
EXAMPLES: MULTILEVEL MIXTURE MODELING
Multilevel mixture modeling (Asparouhov & Muthén, 2008a) combines the multilevel and mixture models by allowing not only the modeling of multilevel data but also the modeling of subpopulations where population membership is not known but is inferred from the data. Mixture modeling can be combined with the multilevel analyses discussed in Chapter 9. Observed outcome variables can be continuous, censored, binary, ordered categorical (ordinal), unordered categorical (nominal), counts, or combinations of these variable types.
With cross-sectional data, the number of levels in Mplus is the same as the number of levels in conventional multilevel modeling programs. Mplus allows two-level modeling. With longitudinal data, the number of levels in Mplus is one less than the number of levels in conventional multilevel modeling programs because Mplus takes a multivariate approach to repeated measures analysis. Longitudinal models are two-level models in conventional multilevel programs, whereas they are one-level models in Mplus. Single-level longitudinal models are discussed in Chapter 6, and single-level longitudinal mixture models are discussed in Chapter 8. Three-level longitudinal analysis where time is the first level, individual is the second level, and cluster is the third level is handled by two-level growth modeling in Mplus as discussed in Chapter 9.
Multilevel mixture models can include regression analysis, path analysis, confirmatory factor analysis (CFA), item response theory (IRT) analysis, structural equation modeling (SEM), latent class analysis (LCA), latent transition analysis (LTA), latent class growth analysis (LCGA), growth mixture modeling (GMM), discrete-time survival analysis, continuous-time survival analysis, and combinations of these models.
All multilevel mixture models can be estimated using the following special features:
· Single or multiple group analysis
· Missing data
· Complex survey data
· Latent variable interactions and non-linear factor analysis using maximum likelihood
· Random slopes
· Individually-varying times of observations
· Linear and non-linear parameter constraints
· Maximum likelihood estimation for all outcome types
· Wald chi-square test of parameter equalities
· Analysis with between-level categorical latent variables
· Test of equality of means across latent classes using posterior probability-based multiple imputations
For TYPE=MIXTURE, multiple group analysis is specified by using the KNOWNCLASS option of the VARIABLE command. The default is to estimate the model under missing data theory using all available data. The LISTWISE option of the DATA command can be used to delete all observations from the analysis that have missing values on one or more of the analysis variables. Corrections to the standard errors and chi-square test of model fit that take into account stratification, non-independence of observations, and unequal probability of selection are obtained by using the TYPE=COMPLEX option of the ANALYSIS command in conjunction with the STRATIFICATION, CLUSTER, WEIGHT, WTSCALE, BWEIGHT, and BWTSCALE options of the VARIABLE command. Latent variable interactions are specified by using the | symbol of the MODEL command in conjunction with the XWITH option of the MODEL command. Random slopes are specified by using the | symbol of the MODEL command in conjunction with the ON option of the MODEL command. Individually-varying times of observations are specified by using the | symbol of the MODEL command in conjunction with the AT option of the MODEL command and the TSCORES option of the VARIABLE command. Linear and non-linear parameter constraints are specified by using the MODEL CONSTRAINT command. Maximum likelihood estimation is specified by using the ESTIMATOR option of the ANALYSIS command. The MODEL TEST command is used to test linear restrictions on the parameters in the MODEL and MODEL CONSTRAINT commands using the Wald chi-square test. Between-level categorical latent variables are specified using the CLASSES and BETWEEN options of the VARIABLE command. The AUXILIARY option is used to test the equality of means across latent classes using posterior probability-based multiple imputations.
Graphical displays of observed data and analysis results can be obtained using the PLOT command in conjunction with a post-processing graphics module. The PLOT command provides histograms, scatterplots, plots of individual observed and estimated values, and plots of sample and estimated means and proportions/probabilities. These are available for the total sample, by group, by class, and adjusted for covariates. The PLOT command includes a display showing a set of descriptive statistics for each variable. The graphical displays can be edited and exported as a DIB, EMF, or JPEG file. In addition, the data for each graphical display can be saved in an external file for use by another graphics program.
Following is the set of cross-sectional examples included in this chapter:
· 10.1: Two-level mixture regression for a continuous dependent variable*
· 10.2: Two-level mixture regression for a continuous dependent variable with a between-level categorical latent variable*
· 10.3: Two-level mixture regression for a continuous dependent variable with between-level categorical latent class indicators for a between-level categorical latent variable*
· 10.4: Two-level CFA mixture model with continuous factor indicators*
· 10.5: Two-level IRT mixture analysis with binary factor indicators and a between-level categorical latent variable*
· 10.6: Two-level LCA with categorical latent class indicators with covariates*
· 10.7: Two-level LCA with categorical latent class indicators and a between-level categorical latent variable
Following is the set of longitudinal examples included in this chapter:
· 10.8: Two-level growth model for a continuous outcome (three-level analysis) with a between-level categorical latent variable*
· 10.9: Two-level GMM for a continuous outcome (three-level analysis)*
· 10.10: Two-level GMM for a continuous outcome (three-level analysis) with a between-level categorical latent variable*
· 10.11: Two-level LCGA for a three-category outcome*
· 10.12: Two-level LTA with a covariate*
· 10.13: Two-level LTA with a covariate and a between-level categorical latent variable
* Example uses numerical integration in the estimation of the model. This can be computationally demanding depending on the size of the problem.
TITLE: this is an example of a two-level mixture regression for a continuous dependent variable
DATA: FILE IS ex10.1.dat;
VARIABLE: NAMES ARE y x1 x2 w class clus;
USEVARIABLES = y x1 x2 w;
CLASSES = c (2);
WITHIN = x1 x2;
BETWEEN = w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
STARTS = 0;
MODEL:
%WITHIN%
%OVERALL%
y ON x1 x2;
c ON x1;
%c#1%
y ON x2;
y;
%BETWEEN%
%OVERALL%
y ON w;
c#1 ON w;
c#1*1;
%c#1%
[y*2];
OUTPUT: TECH1 TECH8;
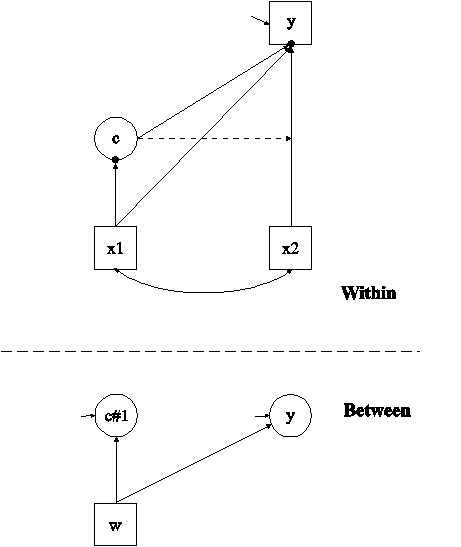
In this example, the two-level mixture regression model for a continuous dependent variable shown in the picture above is estimated. This example is the same as Example 7.1 except that it has been extended to the multilevel framework. In the within part of the model, the filled circles at the end of the arrows from x1 to c and y represent random intercepts that are referred to as c#1 and y in the between part of the model. In the between part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters. The random intercepts y and c#1 are regressed on a cluster-level covariate w.
Because c is a categorical latent variable, the interpretation of the picture is not the same as for models with continuous latent variables. The arrow from c to the y variable indicates that the intercept of the y variable varies across the classes of c. This corresponds to the regression of y on a set of dummy variables representing the categories of c. The broken arrow from c to the arrow from x2 to y indicates that the slope in the linear regression of y on x2 varies across the classes of c. The arrow from x1 to c represents the multinomial logistic regression of c on x1.
TITLE: this is an example of a two-level mixture regression for a continuous dependent variable
The TITLE command is used to provide a title for the analysis. The title is printed in the output just before the Summary of Analysis.
DATA: FILE IS ex10.1.dat;
The DATA command is used to provide information about the data set to be analyzed. The FILE option is used to specify the name of the file that contains the data to be analyzed, ex10.1.dat. Because the data set is in free format, the default, a FORMAT statement is not required.
VARIABLE: NAMES ARE y x1 x2 w class clus;
USEVARIABLES = y x1 x2 w;
CLASSES = c (2);
WITHIN = x1 x2;
BETWEEN = w;
CLUSTER = clus;
The VARIABLE command is used to provide information about the variables in the data set to be analyzed. The NAMES option is used to assign names to the variables in the data set. The data set in this example contains six variables: y, x1, x2, w, c, and clus. If not all of the variables in the data set are used in the analysis, the USEVARIABLES option can be used to select a subset of variables for analysis. Here the variables y1, x1, x2, and w have been selected for analysis. The CLASSES option is used to assign names to the categorical latent variables in the model and to specify the number of latent classes in the model for each categorical latent variable. In the example above, there is one categorical latent variable c that has two latent classes. The WITHIN option is used to identify the variables in the data set that are measured on the individual level and modeled only on the within level. They are specified to have no variance in the between part of the model. The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level and modeled only on the between level. Variables not mentioned on the WITHIN or the BETWEEN statements are measured on the individual level and can be modeled on both the within and between levels. The CLUSTER option is used to identify the variable that contains cluster information.
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
STARTS = 0;
The ANALYSIS command is used to describe the technical details of the analysis. The TYPE option is used to describe the type of analysis that is to be performed. By selecting TWOLEVEL MIXTURE, a multilevel mixture model will be estimated. By specifying STARTS=0 in the ANALYSIS command, random starts are turned off.
MODEL:
%WITHIN%
%OVERALL%
y ON x1 x2;
c ON x1;
%c#1%
y ON x2;
y;
%BETWEEN%
%OVERALL%
y ON w;
c#1 ON w;
c#1*1;
%c#1%
[y*2];
The MODEL command is used to describe the model to be estimated. In multilevel models, a model is specified for both the within and between parts of the model. For mixture models, there is an overall model designated by the label %OVERALL%. The overall model describes the part of the model that is in common for all latent classes. The part of the model that differs for each class is specified by a label that consists of the categorical latent variable name followed by the number sign (#) followed by the class number. In the example above, the label %c#2% refers to the part of the model for class 2 that differs from the overall model.
In the overall model in the within part of the model, the first ON statement describes the linear regression of y on the individual-level covariates x1 and x2. The second ON statement describes the multinomial logistic regression of the categorical latent variable c on the individual-level covariate x1 when comparing class 1 to class 2. The intercept in the regression of c on x1 is estimated as the default. In the model for class 1 in the within part of the model, the ON statement describes the linear regression of y on the individual-level covariate x2 which relaxes the default equality of regression coefficients across classes. By mentioning the residual variance of y, it is not held equal across classes.
In the overall model in the between part of the model, the first ON statement describes the linear regression of the random intercept y on the cluster-level covariate w. The second ON statement describes the linear regression of the random intercept c#1 of the categorical latent variable c on the cluster-level covariate w. The random intercept c#1 is a continuous latent variable. Each class of the categorical latent variable c except the last class has a random intercept. A starting value of one is given to the residual variance of the random intercept c#1. In the class-specific part of the between part of the model, the intercept of y is given a starting value of 2 for class 1.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator.
Following is an alternative specification of the multinomial logistic regression of c on the individual-level covariate x1 in the within part of the model:
c#1 ON x1;
where c#1 refers to the first class of c. The classes of a categorical latent variable are referred to by adding to the name of the categorical latent variable the number sign (#) followed by the number of the class. This alternative specification allows individual parameters to be referred to in the MODEL command for the purpose of giving starting values or placing restrictions.
OUTPUT: TECH1 TECH8;
The OUTPUT command is used to request additional output not included as the default. The TECH1 option is used to request the arrays containing parameter specifications and starting values for all free parameters in the model. The TECH8 option is used to request that the optimization history in estimating the model be printed in the output. TECH8 is printed to the screen during the computations as the default. TECH8 screen printing is useful for determining how long the analysis takes.
TITLE: this is an example of a two-level mixture
regression for a continuous dependent variable with a between-level categorical latent variable
DATA: FILE = ex10.2.dat;
VARIABLE: NAMES ARE y x1 x2 w dummy clus;
USEVARIABLES = y-w;
CLASSES = cb(2);
WITHIN = x1 x2;
BETWEEN = cb w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE RANDOM;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
s1 | y ON x1;
s2 | y ON x2;
%BETWEEN%
%OVERALL%
cb y ON w; s1-s2@0;
%cb#1%
[s1 s2];
%cb#2%
[s1 s2];
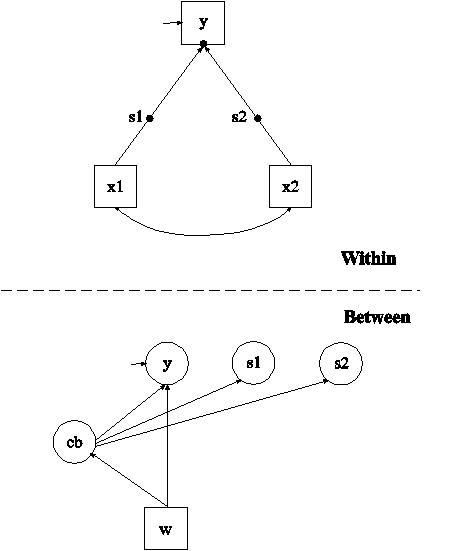
In this example, the two-level mixture regression model for a continuous dependent variable shown in the picture above is estimated. This example is similar to Example 10.1 except that the categorical latent variable is a between-level variable. This means that latent classes are formed for clusters (between-level units) not individuals. In addition, the regression slopes are random not fixed. In the within part of the model, the random intercept is shown in the picture as a filled circle at the end of the arrow pointing to y. It is referred to as y on the between level. The random slopes are shown as filled circles on the arrows from x1 and x2 to y. They are referred to as s1 and s2 on the between level. The random effects y, s1, and s2 are shown in circles in the between part of the model because they are continuous latent variables that vary across clusters (between-level units). In the between part of the model, the arrows from cb to y, s1, and s2 indicate that the intercept of y and the means of s1 and s2 vary across the classes of cb. In addition, the random intercept y and the categorical latent variable cb are regressed on a cluster-level covariate w. The random slopes s1 and s2 have no within-class variance. Only their means vary across the classes of cb. This implies that the distributions of s1 and s2 can be thought of as non-parametric representations rather than normal distributions (Aitkin, 1999; Muthén & Asparouhov, 2009). Another example of a non-parametric representation of a latent variable distribution is shown in Example 7.26.
The BETWEEN option is used to identify the variables in the data set that are measured on the cluster level and modeled only on the between level and to identify between-level categorical latent variables. In this example, the categorical latent variable cb is a between-level variable. Between-level classes consist of clusters such as schools instead of individuals. The PROCESSORS option of the ANALYSIS command is used to specify that 2 processors will be used in the analysis for parallel computations.
In the overall part of the within part of the model, the | symbol is used in conjunction with TYPE=RANDOM to name and define the random slope variables in the model. The name on the left-hand side of the | symbol names the random slope variable. The statement on the right-hand side of the | symbol defines the random slope variable. Random slopes are defined using the ON option. The random slopes s1 and s2 are defined by the linear regressions of the dependent variable y on the individual-level covariates x1 and x2. The within-level residual variance in the regression of y on x is estimated as the default.
In the overall part of the between part of the model, the ON statement describes the multinomial logistic regression of the categorical latent variable cb on the cluster-level covariate w and the linear regression of the random intercept y on the cluster-level covariate w. The variances of the random slopes s1 and s2 are fixed at zero. In the class-specific parts of the between part of the model, the means of the random slopes are specified to vary across the between-level classes of cb. The intercept of the random intercept y varies across the between-level classes of cb as the default.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with a total of 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 10.1.
Following is an alternative specification of the MODEL command that is simpler when the model has many covariates and when the variances of the random slopes are zero:
MODEL:
%WITHIN%
%OVERALL%
y ON x1 x2;
%cb#1%
y ON x1 x2;
%cb#2%
y ON x1 x2;
%BETWEEN%
%OVERALL%
cb ON w;
y ON w;
In this specification, instead of the | statements, the random slopes are represented as class-varying slopes in the class-specific parts of the within part of the model. This specification makes it unnecessary to refer to the means and variances of the random slopes in the between part of the model.
TITLE: this is an example of a two-level mixture
regression for a continuous dependent variable with between-level categorical latent class indicators for a between-level categorical latent variable
DATA: FILE = ex10.3.dat;
VARIABLE: NAMES ARE u1-u6 y x1 x2 w dummy clus;
USEVARIABLES = u1-w;
CATEGORICAL = u1-u6;
CLASSES = cb(2);
WITHIN = x1 x2;
BETWEEN = cb w u1-u6;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
y ON x1 x2;
%BETWEEN%
%OVERALL%
cb ON w;
y ON w;
OUTPUT: TECH1 TECH8;
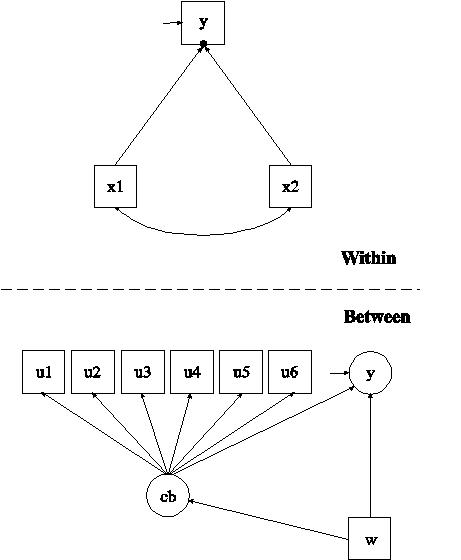
In this example, the two-level mixture regression model for a continuous dependent variable shown in the picture above is estimated. This example is similar to Example 10.2 except that the between-level categorical latent variable has between-level categorical latent class indicators and the slopes are fixed. In the within part of the model, the random intercept is shown in the picture as a filled circle at the end of the arrow pointing to y. It is referred to as y on the between level. The random intercept y is shown in a circle in the between part of the model because it is a continuous latent variable that varies across clusters (between-level units). In the between part of the model, the arrow from cb to y indicates that the intercept of y varies across the classes of cb. In addition, the random intercept y and the categorical latent variable cb are regressed on a cluster-level covariate w. The arrows from cb to u1, u2, u3, u4, u5, and u6 indicate that these variables are between-level categorical latent class indicators of the categorical latent variable cb.
In the overall part of the between part of the model, the first ON statement describes the multinomial logistic regression of the categorical latent variable cb on the cluster-level covariate w. The second ON statement describes the linear regression of the random intercept y on the cluster-level covariate w. The intercept of the random intercept y and the thresholds of the between-level latent class indicators u1, u2, u3, u4, u5, and u6 vary across the between-level classes of cb as the default.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with a total of 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 10.1 and 10.2.
TITLE: this is an example of a two-level CFA mixture model with continuous factor indicators
DATA: FILE IS ex10.4.dat;
VARIABLE: NAMES ARE y1-y5 class clus;
USEVARIABLES = y1-y5;
CLASSES = c (2);
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
STARTS = 0;
MODEL:
%WITHIN%
%OVERALL%
fw BY y1-y5;
%BETWEEN%
%OVERALL%
fb BY y1-y5;
c#1*1;
%c#1%
[fb*2];
OUTPUT: TECH1 TECH8;
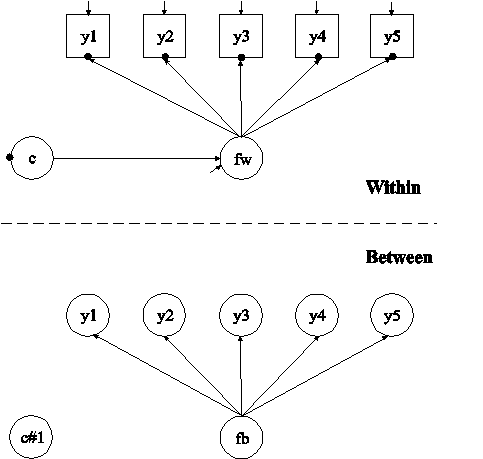
In this example, the two-level confirmatory factor analysis (CFA) mixture model with continuous factor indicators in the picture above is estimated. This example is the same as Example 7.17 except that it has been extended to the multilevel framework. In the within part of the model, the filled circles at the end of the arrows from the within factor fw to y1, y2, y3, y4, and y5 represent random intercepts that vary across clusters. The filled circle on the circle containing c represents the random mean of c that varies across clusters. In the between part of the model, the random intercepts are referred to as y1, y2, y3, y4, and y5 and the random mean is referred to as c#1 where they are shown in circles because they are continuous latent variables that vary across clusters. In the between part of the model, the random intercepts are indicators of the between factor fb. In this model, the residual variances for the factor indicators in the between part of the model are zero. If factor loadings are constrained to be equal across the within and the between levels, this implies a model where the mean of the within factor varies across the clusters. The between part of the model specifies that the random mean c#1 of the categorical latent variable c and the between factor fb are uncorrelated. Other modeling possibilities are for fb and c#1 to be correlated, for fb to be regressed on c#1, or for c#1 to be regressed on fb. Regressing c#1 on fb, however, leads to an internally inconsistent model where the mean of fb is influenced by c at the same time as c#1 is regressed on fb, leading to a reciprocal interaction.
In the overall part of the within part of the model, the BY statement specifies that fw is measured by the factor indicators y1, y2, y3, y4, and y5. The metric of the factor is set automatically by the program by fixing the first factor loading to one. This option can be overridden. The residual variances of the factor indicators are estimated and the residuals are not correlated as the default. The variance of the factor is estimated as the default.
In the overall part of the between part of the model, the BY statement specifies that fb is measured by the random intercepts y1, y2, y3, y4, and y5. The residual variances of the random intercepts are fixed at zero as the default because they are often very small and each residual variance requires one dimension of numerical integration. The variance of fb is estimated as the default. A starting value of one is given to the variance of the random mean of the categorical latent variable c referred to as c#1. In the model for class 1 in the between part of the model, the mean of fb is given a starting value of 2.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 10.1.
TITLE: this is an example of a two-level IRT mixture analysis with binary factor indicators and a between-level categorical latent variable
DATA: FILE = ex10.5.dat;
VARIABLE: NAMES ARE u1-u8 dumb dum clus;
USEVARIABLES = u1-u8;
CATEGORICAL = u1-u8;
CLASSES = cb(2) c(2);
BETWEEN = cb;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
ALGORITHM = INTEGRATION;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
f BY u1-u8;
[f@0];
%BETWEEN%
%OVERALL%
%cb#1.c#1%
[u1$1-u8$1];
%cb#1.c#2%
[u1$1-u8$1];
%cb#2.c#1%
[u1$1-u8$1];
%cb#2.c#2%
[u1$1-u8$1];
MODEL c:
%WITHIN%
%c#1%
f;
%c#2%
f;
OUTPUT: TECH1 TECH8;
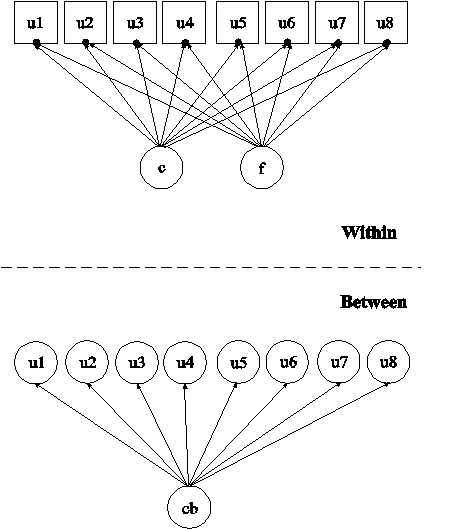
In this example, the two-level item response theory (IRT) mixture model with binary factor indicators shown in the picture above is estimated. The model has both individual-level classes and between-level classes. Individual-level classes consist of individuals, for example, students. Between-level classes consist of clusters, for example, schools. The within part of the model is similar to the single-level model in Example 7.27. In the within part of the model, an IRT mixture model is specified where the factor indicators u1, u2, u3, u4, u5, u6, u7, and u8 have thresholds that vary across the classes of the individual-level categorical latent variable c. The filled circles at the end of the arrows pointing to the factor indicators show that the thresholds of the factor indicators are random. They are referred to as u1, u2, u3, u4, u5, u6, u7, and u8 on the between level. The random thresholds u1, u2, u3, u4, u5, u6, u7, and u8 are shown in circles in the between part of the model because they are continuous latent variables that vary across clusters (between-level units). The random thresholds have no within-class variance. They vary across the classes of the between-level categorical latent variable cb. For related models, see Asparouhov and Muthén (2008a).
In the class-specific part of the between part of the model, the random thresholds are specified to vary across classes that are a combination of the classes of the between-level categorical latent variable cb and the individual-level categorical latent variable c. These classes are referred to by combining the class labels using a period (.). For example, a combination of class 1 of cb and class 1 of c is referred to as cb#1.c#1. This represents an interaction between the two categorical latent variables in their influence on the thresholds.
When a model has more than one categorical latent variable, MODEL followed by a label is used to describe the analysis model for each categorical latent variable. Labels are defined by using the names of the categorical latent variables. In the model for the individual-level categorical latent variable c, the variances of the factor f are allowed to vary across the classes of c.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with a total of 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 7.27, 10.1, and 10.2.
TITLE: this is an example of a two-level LCA with categorical latent class indicators with covariates
DATA: FILE IS ex10.6.dat;
VARIABLE: NAMES ARE u1-u6 x w class clus;
USEVARIABLES = u1-u6 x w;
CATEGORICAL = u1-u6;
CLASSES = c (3);
WITHIN = x;
BETWEEN = w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
MODEL:
%WITHIN%
%OVERALL%
c ON x;
%BETWEEN%
%OVERALL%
f BY c#1 c#2;
f ON w;
OUTPUT: TECH1 TECH8;
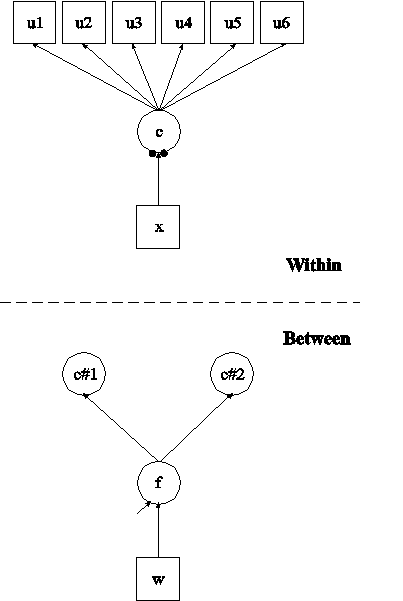
In this example, the two-level latent class analysis (LCA) with categorical latent class indicators and covariates shown in the picture above is estimated (Vermunt, 2003). This example is similar to Example 7.12 except that it has been extended to the multilevel framework. In the within part of the model, the categorical latent variable c is regressed on the individual-level covariate x. The filled circles at the end of the arrow from x to c represent the random intercepts for classes 1 and 2 of the categorical latent variable c which has three classes. The random intercepts are referred to as c#1 and c#2 in the between part of the model where they are shown in circles instead of squares because they are continuous latent variables that vary across clusters. Because the random intercepts in LCA are often highly correlated and to reduce the dimensions of integration, a factor is used to represent the random intercept variation. This factor is regressed on the cluster-level covariate w.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the latent class indicators u1, u2, u3, u4, u5, and u6 are binary or ordered categorical variables. The program determines the number of categories for each indicator.
In the within part of the model, the ON statement describes the multinomial logistic regression of the categorical latent variable c on the individual-level covariate x when comparing classes 1 and 2 to class 3. The intercepts of the random intercepts in the regression of c on x are estimated as the default. The random intercept for class 3 is zero because it is the reference class. In the between part of the model, the BY statement specifies that f is measured by the random intercepts c#1 and c#2. The metric of the factor is set automatically by the program by fixing the first factor loading to one. The residual variances of the random intercepts are fixed at zero as the default. The ON statement describes the linear regression of the between factor f on the cluster-level covariate w.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 10.1.
TITLE: this is an example of a two-level LCA with categorical latent class indicators and a between-level categorical latent variable
DATA: FILE = ex10.7.dat;
VARIABLE: NAMES ARE u1-u10 dumb dumw clus;
USEVARIABLES = u1-u10;
CATEGORICAL = u1-u10;
CLASSES = cb(5) cw(4);
WITHIN = u1-u10;
BETWEEN = cb;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
PROCESSORS = 2;
STARTS = 100 10;
MODEL:
%WITHIN%
%OVERALL%
%BETWEEN%
%OVERALL%
cw#1-cw#3 ON cb;
MODEL cw:
%WITHIN%
%cw#1%
[u1$1-u10$1];
[u1$2-u10$2];
%cw#2%
[u1$1-u10$1];
[u1$2-u10$2];
%cw#3%
[u1$1-u10$1];
[u1$2-u10$2];
%cw#4%
[u1$1-u10$1];
[u1$2-u10$2];
OUTPUT: TECH1 TECH8;
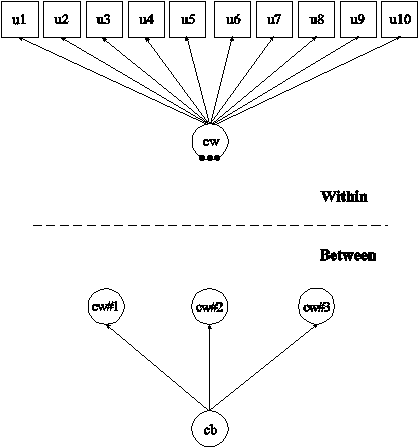
In this example, the two-level latent class analysis (LCA) with categorical latent class indicators shown in the picture above is estimated. This example is similar to Example 10.6 except that the between level random means are influenced by the between-level categorical latent variable cb. In the within part of the model, the filled circles represent the three random means of the four classes of the individual-level categorical latent variable cw. They are referred to as cw#1, cw#2, and cw#3 on the between level. The random means are shown in circles in the between part of the model because they are continuous latent variables that vary across clusters (between-level units). The random means have means that vary across the classes of the categorical latent variable cb but the within-class variances of the random means are zero (Bijmolt, Paas, & Vermunt, 2004).
In the overall part of the between part of the model, the ON statement describes the linear regressions of cw#1, cw#2, and cw#3 on the between-level categorical latent variable cb. This regression implies that the means of these random means vary across the classes of the categorical latent variable cb.
The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 10.1, 10.2, and 10.6.
TITLE: this is an example of a two-level growth
model for a continuous outcome (three-
level analysis) with a between-level categorical latent variable
DATA: FILE = ex10.8.dat;
VARIABLE: NAMES ARE y1-y4 x w dummy clus;
USEVARIABLES = y1-w;
CLASSES = cb(2);
WITHIN = x;
BETWEEN = cb w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE RANDOM;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
iw sw | y1@0 y2@1 y3@2 y4@3;
y1-y4 (1);
iw sw ON x;
s | sw ON iw;
%BETWEEN%
%OVERALL%
ib sb | y1@0 y2@1 y3@2 y4@3;
y1-y4@0;
ib sb ON w;
cb ON w;
s@0;
%cb#1%
[ib sb s];
%cb#2%
[ib sb s];
OUTPUT: TECH1 TECH8;

In this example, the two-level growth model for a continuous outcome (three-level analysis) shown in the picture above is estimated. This example is similar to Example 9.12 except that a random slope is estimated in the within-level regression of the slope growth factor on the intercept growth factor and a between-level latent class variable cb is part of the model. This means that latent classes are formed for clusters (between-level units) not individuals. In the within part of the model, the random slope is shown in the picture as a filled circle on the arrow from iw to sw. It is referred to as s on the between level. The random slope s is shown in a circle in the between part of the model because it is a continuous latent variable that varies across clusters (between-level units). In the between part of the model, the arrows from cb to ib, sb, and s indicate that the intercepts of ib and sb and the mean of s vary across the classes of cb. In addition, the categorical latent variable cb is regressed on a cluster-level covariate w. The random slope s has no within-class variance. Only its mean varies across the classes of cb. This implies that the distributions of s can be thought of as a non-parametric representation rather than a normal distribution (Aitkin, 1999; Muthén & Asparouhov, 2007).
In the overall part of the within part of the model, the | statement is used to name and define the random slope s which is used in the between part of the model. In the overall part of the between part of the model, the second ON statement describes the multinomial logistic regression of the categorical latent variable cb on a cluster-level covariate w. The variance of the random slope s is fixed at zero. In the class-specific parts of the between part of the model, the intercepts of the growth factors ib and sb and the mean of the random slope s are specified to vary across the between-level classes of cb.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 9.12, 10.1, and 10.2.
Following is an alternative specification of the MODEL command that is simpler when the variances of the random slopes are zero:
MODEL:
%WITHIN%
%OVERALL%
iw sw | y1@0 y2@1 y3@2 y4@3;
y1-y4 (1);
iw ON x;
sw ON x iw;
%cb#1%
sw ON iw;
%cb#2%
sw ON iw;
%BETWEEN%
%OVERALL%
ib sb | y1@0 y2@1 y3@2 y4@3;
y1-y4@0;
ib sb ON w;
cb ON w;
%cb#1%
[ib sb];
%cb#2%
[ib sb];
In this specification, instead of the | statement, the random slope is represented as class-varying slopes in the class-specific parts of the within part of the model. This specification makes it unnecessary to refer to the means and variances of the random slopes in the between part of the model.
TITLE: this is an example of a two-level GMM for a continuous outcome (three-level analysis)
DATA: FILE IS ex10.9.dat;
VARIABLE: NAMES ARE y1-y4 x w class clus;
USEVARIABLES = y1-y4 x w;
CLASSES = c (2);
WITHIN = x;
BETWEEN = w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
STARTS = 0;
MODEL:
%WITHIN%
%OVERALL%
iw sw | y1@0 y2@1 y3@2 y4@3;
iw sw ON x;
c ON x;
%BETWEEN%
%OVERALL%
ib sb | y1@0 y2@1 y3@2 y4@3;
y1-y4@0;
ib sb ON w;
sb@0;
c#1 ON w;
c#1*1;
%c#1%
[ib sb];
%c#2%
[ib*3 sb*1];
OUTPUT: TECH1 TECH8;

In this example, the two-level growth mixture model (GMM; Muthén, 2004; Muthén & Asparouhov, 2009) for a continuous outcome (three-level analysis) shown in the picture above is estimated. This example is similar to Example 8.1 except that it has been extended to the multilevel framework. In the within part of the model, the filled circles at the end of the arrows from the within growth factors iw and sw to y1, y2, y3, and y4 represent random intercepts that vary across clusters. The filled circle at the end of the arrow from x to c represents a random intercept. The random intercepts are referred to in the between part of the model as y1, y2, y3, y4, and c#1. In the between-part of the model, the random intercepts are shown in circles because they are continuous latent variables that vary across clusters.
In the within part of the model, the | statement names and defines the within intercept and slope factors for the growth model. The names iw and sw on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The values on the right-hand side of the | symbol are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are estimated and allowed to be different across time and the residuals are not correlated as the default. The first ON statement describes the linear regressions of the growth factors on the individual-level covariate x. The residual variances of the growth factors are free to be estimated as the default. The residuals of the growth factors are correlated as the default because residuals are correlated for latent variables that do not influence any other variable in the model except their own indicators. The second ON statement describes the multinomial logistic regression of the categorical latent variable c on the individual-level covariate x when comparing class 1 to class 2. The intercept in the regression of c on x is estimated as the default.
In the overall model in the between part of the model, the | statement names and defines the between intercept and slope factors for the growth model. The names ib and sb on the left-hand side of the | symbol are the names of the intercept and slope growth factors, respectively. The values of the right-hand side of the | symbol are the time scores for the slope growth factor. The time scores of the slope growth factor are fixed at 0, 1, 2, and 3 to define a linear growth model with equidistant time points. The zero time score for the slope growth factor at time point one defines the intercept growth factor as an initial status factor. The coefficients of the intercept growth factor are fixed at one as part of the growth model parameterization. The residual variances of the outcome variables are fixed at zero on the between level in line with conventional multilevel growth modeling. This can be overridden. The first ON statement describes the linear regressions of the growth factors on the cluster-level covariate w. The residual variance of the intercept growth factor is free to be estimated as the default. The residual variance of the slope growth factor is fixed at zero because it is often small and each residual variance requires one dimension of numerical integration. Because the slope growth factor residual variance is fixed at zero, the residual covariance between the growth factors is automatically fixed at zero. The second ON statement describes the linear regression of the random intercept c#1 of the categorical latent variable c on the cluster-level covariate w. A starting value of one is given to the residual variance of the random intercept of the categorical latent variable c referred to as c#1.
In the parameterization of the growth model shown here, the intercepts of the outcome variable at the four time points are fixed at zero as the default. The growth factor intercepts are estimated as the default in the between part of the model. In the model for class 2 in the between part of the model, the mean of ib and sb are given a starting value of zero in class 1 and three and one in class 2.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 10.1.
TITLE: this is an example of a two-level GMM for a continuous outcome (three-level analysis) with a between-level categorical latent variable
DATA: FILE = ex10.10.dat;
VARIABLE: NAMES ARE y1-y4 x w dummyb dummy clus;
USEVARIABLES = y1-w;
CLASSES = cb(2) c(2);
WITHIN = x;
BETWEEN = cb w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
iw sw | y1@0 y2@1 y3@2 y4@3;
iw sw ON x;
c ON x;
%BETWEEN%
%OVERALL%
ib sb | y1@0 y2@1 y3@2 y4@3;
ib2 | y1-y4@1;
y1-y4@0;
ib sb ON w;
c#1 ON w;
sb@0; c#1;
ib2@0;
cb ON w;
MODEL c:
%BETWEEN%
%c#1%
[ib sb];
%c#2%
[ib sb];
MODEL cb:
%BETWEEN%
%cb#1%
[ib2@0];
%cb#2%
[ib2];
OUTPUT: TECH1 TECH8;

In this example, the two-level growth mixture model (GMM; Muthén & Asparouhov, 2009) for a continuous outcome (three-level analysis) shown in the picture above is estimated. This example is similar to Example 10.9 except that a between-level categorical latent variable cb has been added along with a second between-level intercept growth factor ib2. The second intercept growth factor is added to the model so that the intercept growth factor mean can vary across not only the classes of the individual-level categorical latent variable c but also across the classes of the between-level categorical latent variable cb. Individual-level classes consist of individuals, for example, students. Between-level classes consist of clusters, for example, schools.
In the overall part of the between part of the model, the second | statement names and defines the second between-level intercept growth factor ib2. This growth factor is used to represent differences in intercept growth factor means across the between-level classes of the categorical latent variable cb.
When a model has more than one categorical latent variable, MODEL followed by a label is used to describe the analysis model for each categorical latent variable. Labels are defined by using the names of the categorical latent variables. In the model for the individual-level categorical latent variable c, the intercepts of the intercept and slope growth factors ib and sb are allowed to vary across the classes of the individual-level categorical latent variable c. In the model for the between-level categorical latent variable cb, the means of the intercept growth factor ib2 are allowed to vary across clusters (between-level units). The mean in one class is fixed at zero for identification purposes.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 10.1, 10.2, and 10.4.
TITLE: this is an example of a two-level LCGA for a three-category outcome
DATA: FILE IS ex10.11.dat;
VARIABLE: NAMES ARE u1-u4 class clus;
USEVARIABLES = u1-u4;
CATEGORICAL = u1-u4;
CLASSES = c(2);
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
MODEL:
%WITHIN%
%OVERALL%
i s | u1@0 u2@1 u3@2 u4@3;
i-s@0;
%c#1%
[i*1 s*1];
%c#2%
[i@0 s];
%BETWEEN%
%OVERALL%
c#1*1;
[u1$1-u4$1*1] (1);
[u1$2-u4$2*1.5] (2);
OUTPUT: TECH1 TECH8;
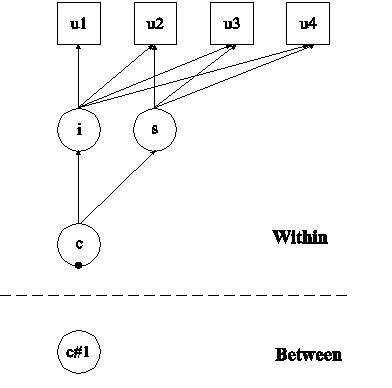
In this example, the two-level latent class growth analysis (LCGA) shown in the picture above is estimated. This example is the same as Example 8.10 except that it has been extended to the multilevel framework. A growth model is not specified in the between part of the model because the variances of the growth factors i and s are zero in LCGA. The filled circle on the circle containing the categorical latent variable c represents the random mean of c. In the between part of the model, the random mean is shown in a circle because it is a continuous latent variable that varies across clusters.
The CATEGORICAL option is used to specify which dependent variables are treated as binary or ordered categorical (ordinal) variables in the model and its estimation. In the example above, the latent class indicators u1, u2, u3, u4, u5, and u6 are binary or ordered categorical variables. The program determines the number of categories for each indicator. In this example, u1, u2, u3, and u4 are three-category variables.
In the overall part of the of the within part of the model, the variances of the growth factors i and s are fixed at zero because latent class growth analysis has no within class variability. In the overall part of the of the between part of the model, the two thresholds for the outcome are held equal across the four time points. The growth factor means are specified in the within part of the model because there are no between growth factors.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, one dimension of integration is used with 15 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Example 10.1.
TITLE: this is an example of a two-level LTA with a covariate
DATA: FILE = ex10.12.dat;
VARIABLE: NAMES ARE u11-u14 u21-u24 x w dum1 dum2 clus;
USEVARIABLES = u11-w;
CATEGORICAL = u11-u14 u21-u24;
CLASSES = c1(2) c2(2);
WITHIN = x;
BETWEEN = w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
c2 ON c1 x;
c1 ON x;
%BETWEEN%
%OVERALL%
c1#1 ON w;
c2#1 ON c1#1 w;
c1#1 c2#1;
MODEL c1:
%BETWEEN%
%c1#1%
[u11$1-u14$1] (1-4);
%c1#2%
[u11$1-u14$1] (5-8);
MODEL c2:
%BETWEEN%
%c2#1%
[u21$1-u24$1] (1-4);
%c2#2%
[u21$1-u24$1] (5-8);
OUTPUT: TECH1 TECH8;
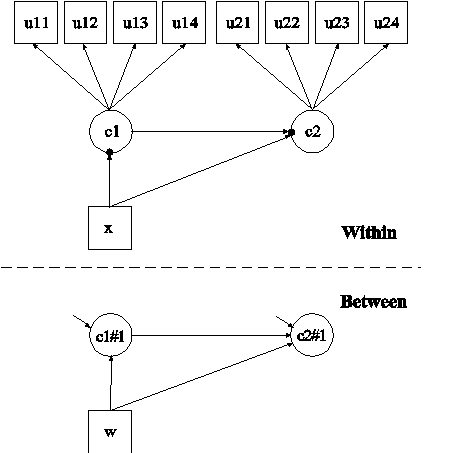
In this example, the two-level latent transition analysis (LTA) with a covariate shown in the picture above is estimated. This example is similar to Example 8.13 except that the categorical latent variables are allowed to have random intercepts that vary on the between level. This model is described in Asparouhov and Muthén (2008a). In the within part of the model, the random intercepts are shown in the picture as filled circles at the end of the arrows pointing to c1 and c2. They are referred to as c1#1 and c2#1 on the between level. The random intercepts c1#1 and c2#1 are shown in circles in the between part of the model because they are continuous latent variables that vary across clusters (between-level units).
In the overall part of the between part of the model, the first ON statement describes the linear regression of the random intercept c1#1 on a cluster-level covariate w. The second ON statement describes the linear regression of the random intercept c2#1 on the random intercept c1#1 and the cluster-level covariate w. The residual variances of the random intercepts c1#1 and c2#1 are estimated instead of being fixed at the default value of zero.
The default estimator for this type of analysis is maximum likelihood with robust standard errors using a numerical integration algorithm. Note that numerical integration becomes increasingly more computationally demanding as the number of factors and the sample size increase. In this example, two dimensions of integration are used with a total of 225 integration points. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 8.13, 10.1, and 10.2.
TITLE: this is an example of a two-level LTA with a covariate and a between-level categorical latent variable
DATA: FILE = ex10.13.dat;
VARIABLE: NAMES ARE u11-u14 u21-u24 x w dumb dum1 dum2 clus;
USEVARIABLES = u11-w;
CATEGORICAL = u11-u14 u21-u24;
CLASSES = cb(2) c1(2) c2(2);
WITHIN = x;
BETWEEN = cb w;
CLUSTER = clus;
ANALYSIS: TYPE = TWOLEVEL MIXTURE;
PROCESSORS = 2;
MODEL:
%WITHIN%
%OVERALL%
c2 ON c1 x;
c1 ON x;
%BETWEEN%
%OVERALL%
c1#1 ON cb;
c2#1 ON cb;
cb ON w;
MODEL cb:
%WITHIN%
%cb#1%
c2 ON c1;
MODEL c1:
%BETWEEN%
%c1#1%
[u11$1-u14$1] (1-4);
%c1#2%
[u11$1-u14$1] (5-8);
MODEL c2:
%BETWEEN%
%c2#1%
[u21$1-u24$1] (1-4);
%c2#2%
[u21$1-u24$1] (5-8);
OUTPUT: TECH1 TECH8;
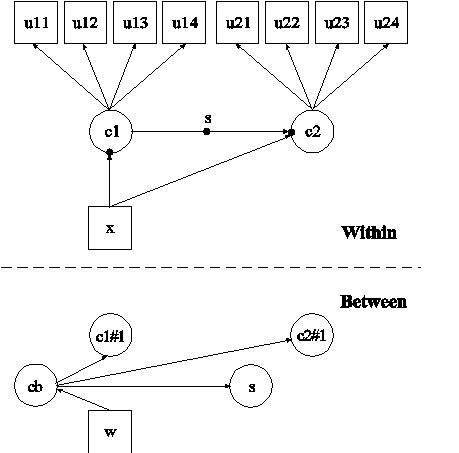
In this example, the two-level latent transition analysis (LTA) with a covariate shown in the picture above is estimated. This example is similar to Example 10.12 except that a between-level categorical latent variable cb has been added, a random slope has been added, and the random intercepts and random slope have no variance within the classes of the between-level categorical latent variable cb (Asparouhov & Muthén, 2008a). In the within part of the model, the random intercepts are shown in the picture as filled circles at the end of the arrows pointing to c1 and c2. The random slope is shown as a filled circle on the arrow from c1 to c2. In the between part of the model, the random intercepts are referred to as c1#1 and c2#1 and the random slope is referred to as s. The random intercepts c1#1 and c2#1 and the random slope s are shown in circles in because they are continuous latent variables that vary across clusters (between-level units). In the between part of the model, the arrows from cb to c1#1, c2#1, and s indicate that the means of c1#1, c2#1, and s vary across the classes of cb.
In the overall part of the between part of the model, the first two ON statements describe the linear regressions of c1#1 and c2#1 on the between-level categorical latent variable cb. These regressions imply that the means of the random intercepts vary across the classes of the categorical latent variable cb. The variances of c1#1 and c2#1 within the cb classes are zero as the default.
When a model has more than one categorical latent variable, MODEL followed by a label is used to describe the analysis model for each categorical latent variable. Labels are defined by using the names of the categorical latent variables. In the class-specific part of the within part of the model for the between-level categorical latent variable cb, the ON statement describes the multinomial regression of c2 on c1. This implies that the random slope s varies across the classes of cb. The within-class variance of s is zero as the default.
The default estimator for this type of analysis is maximum likelihood with robust standard errors. The ESTIMATOR option of the ANALYSIS command can be used to select a different estimator. An explanation of the other commands can be found in Examples 8.13, 10.1, 10.2, and 10.12.